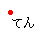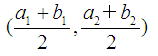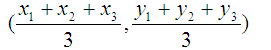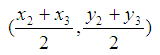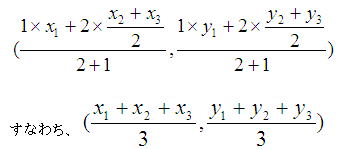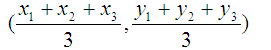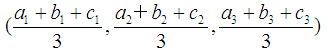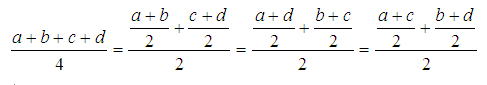重心について考察してみた
(1998年4月17日）

【重心の話の流れ】
●点の重心は a/1である。…（０）
●線分の重心は (a+b)/2である。…（１）
（０）（１）より、
●三角形の重心は中線上に存在する。…（２）
（２）より、
●三角形の中線の交点が重心である。（３）
●三角形の３本の中線は１点で交わり、その点は各中線を２：１に内分する…（４）
（３）（４）より、
●三角形の重心は (a+b+c)/3である。…（５）
●正四面体において、底面の重心と頂点を結んだ線分を１：３に内分する点が重心Gである。…（６）
（５）、（６）より、
●正四面体の重心は(a+b+c+d)/4である。…（７）
●カバリエリの原理…（８）
（７）（８）より
●四面体の重心は (a+b+c+d)/4である。
（７）（８）より
●すべての錐の重心は、
「底面積の重心と頂点を結んだ上にあり、その比は３：１に内分する」

【０　点の重心】
さて、空間に点があったとします。

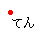
この点の重心は、この点自身です。

【１　線分の重心】
次に、
一本の線分ABがあったとする。
この線分の重心は、中点である。


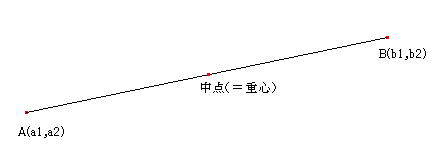
したがって、
座標で言うなら、２点A(a1,a2)，B(b1,b2）の中点の座標は、

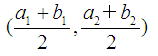
であり、これが重心となる。…★



【２-(1)　三角形の重心】
上記のことから、三角形ABCの頂点を、A(x1,y1),B(x2,y2),C(x3,y3)を頂点とすると
△ABCの重心の座標は

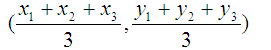
であることが予想される。（←結論から言うと、この予想はアタリ。）

さて、
★より、線分の重心は中点であるので、


上の図より、三角形の場合、
「重心は中線上に存在する。」
ことがわかる。
したがって、２つの頂点から対辺に中線を引き、その交点が重心である。

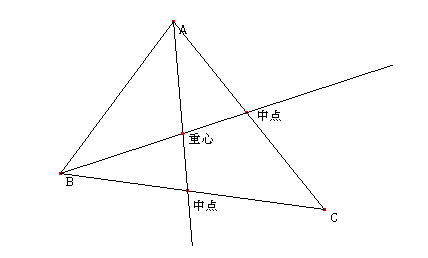
三角形の中線の交点が重心である。

ここで、上記の重心の性質を調べてみる。

△ABCで、ABとACの中点をそれぞれD,Eとし、BEとCDの交点をGとする。

△ADEと△ABCにおいて、
AD：AB=１：２…(1)
AE：AC=１：２…(2)
∠DAE＝∠BAC…(3)
(1)(2)(3)より、１組の辺の比とその間の角が等しいので、
△ADE∽△ABC
よって　DE：BC=１：２

また、△GEDと△GCBにおいて
DE//BCより平行線の錯角が等しいので、
∠GED＝∠GBC…(4)
∠GDE＝∠GCB…(5)
(4)(5)より、二角が等しいので、
△GED∽△GCB
DE：BC=１：２であったから、
BG：GE＝CG：GD=２：１

∠Aの中線についても同様。

以上のことより、
重心は中線を２：１に内分する…(1)
ことがわかる。

また、BCの中点をFとすると、
AFとBEの交点をG’とすると、
線分BEを２：１に内分する点は１点だけであるから、２点G，G'は一致する。
したがって、３つの中線は点Gで交わる。
つまり、
三角形の頂点とその対辺の中点を結ぶ 3 つの線分は 1 点で交わる。…(2)
ことがわかる。

(1)(2)をまとめると、
「三角形の３本の中線は１点で交わり、その点は各中線を２：１に内分する。
ことがいえる。

このことをつかうと、
３点A(x1,y1),B(x2,y2),C(x3,y3)を頂点とする△ABCにおいて、
辺BCの中点をMとすると、
Mの座標は,★より、

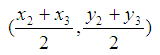
重心Gは線分AMを２：１に内分するから、

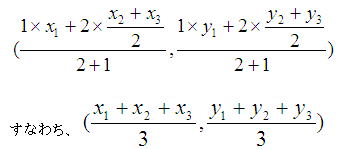
であることがわかる。

以上のことより、
定理：３点A(x1,y1),B(x2,y2),C(x3,y3)を頂点とする△ABCの重心の座標は

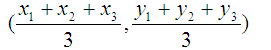
である。

ことがわかる。

同様にして、空間でも同じ理屈で、
三角形ABCの頂点を、３点A(a1,a2,a3),B(b1,b2,b3),C(c1,c2,c3)とすると、
重心は、

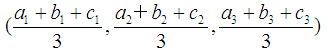
であることがわかる。



【２-(2)　平面上のｎ角形の重心】
ところで、
一角形（点）の重心は、a/1
二角形（線分）の重心は、(a+b)/2
三角形の重心は、(a+b+c)/3
であるということが、これまでの調べでわかった。

この流れで行くと、
四角形の重心は、(a+b+c+d)/4なのではないか？
という予想が出てくる。（←結論から言うと、この予想はハズレ）

もし、四角形の重心が、(a+b+c+d)/4であると仮定すると、


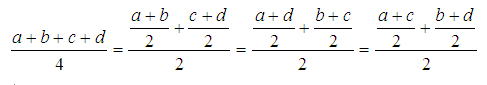
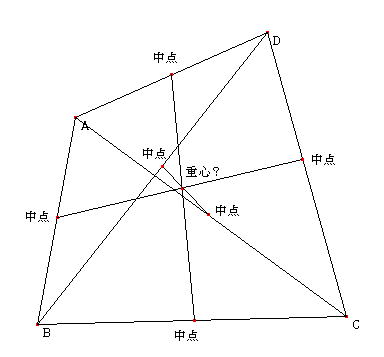
となるので、四角形の各頂点a,b,c,d(←※図のA,B,C,Dのこと)のうちから２つの頂点の組を選び、それら２線分の中点同士の中点が重心であることを意味する。
ここで特殊化してc=dである時のことを考える（つまり三角形であるとき）を考えると、
(a+b+c+d)/4=(a+b+c)/4≠(a+b+c)/3
となり矛盾する。

※…と、説明してみたが、要は、２つの頂点がくっついた場合、そこの比重が２倍になると考えるのは、均一な物質でできた板で考えている今回は、そんなことありえないと言っているだけだ。

だから、上記の図の、たとえば点Bと点Dの中点をとる作業はBとCに重りが乗っている場合の線分BCの重心を意味するわけだが、頂点に重りが乗っていない今回の場合は、これは何の意味もない作業となる。だから当然、これで四角形の重心が求まるはずが無いのである。

(a+b+c+d)/4が意味するのは、頂点に等しい重りをぶら下げたときの重心である。しかし、重りをぶら下げたとはどこにも書いてない！

図形の場合、重心は均一な板で物質ができているときにつりあいの取れる点のことを重心と言っているわけだから、勝手に頂点に重りを乗せて考えてはいけない。

四角形の重心が(a+b+c+d)/4であるという主張は、明らかに、頂点に等しい重さの重りがぶら下がっているという発想から来ているわけだが（あるいは、何も考えず直感的にそうやっているだけの人もいるが…）、当然、この考えだと、頂点以外である図形の中身が考慮されていないことになる。

今回の場合、四角形という図形で考えているわけだから、重心とは図形を等質な重さを持つ板（あるいは物質）で考えなくてはいけないと思うわけで、
与えられた四角形という図形を、頂点に重りがぶら下がっていて、中身はスカスカで細い針金で重心から重りまで結ばれている図形だと、勝手に解釈してはいけない。

一般に、このように重さをぶら下げた場合が物理的重心として言われている場合を数多く見るが、頂点に重りが乗っているとは何処にもかかれていないのに、勝手に頂点に重りをぶら下げ、これのつりあう点を求めて、これをもって、「これが物理的重心だ」と主張するのはおかしいと思う。たしかにそれは、頂点に重りを乗せた場合の重心であることには違いないが。

重心とはつりあいのとれる点のことなのだから、「頂点に重りを載せた場合」と、「乗せない均一な物質でできている場合」の両方を含むのに、前者を物理的重心、後者を数学的重心と区別している傾向が見られる。これが気に入らない。物理的にも数学的にも、重りをぶら下げた場合とそうでない場合のそれぞれの重心をもとめることができるのだから、わざわざそれを、数学的とか物理的と区別するのはそもそもおかしいのである。…と思う。

従って、
「四角形の重心は(a+b+c+d)/4である」と考えるのは間違え
であることがわかった。
（注：三角形の２つの頂点がくっついて、線分になった場合は、
三角形の重心が(a+b+c)/3であることより、特殊化してb=cの場合を考えると、
(a+b+c)/3=(a+b+b)/3=(a+2b)/(2+1)となり、重心は２：１の場所にあることが言える。つまり、三角形の頂点に１ｇの重りがぶら下がっているとして、２つの重りが重なった場合を直線としてみなしたとき、片方に１ｇ、片方に２ｇの重りが乗っていることになる。そして、その重心も２：１で一致する。が、勝手に頂点に重りをぶら下げたと考えてはいけない（←しつこい）。頂点に重りをぶら下げたとして、三角形ではこれが言えてしまうのだが、実はこれはタマタマで、一般の多角形でこれが言えるわけではない。）（恐らく、四角形の重心が(a+b+c+d)/4であるという主張はこの誤解から来ているのだろう。これは、三角形でいえるのだから四角形でも言えるはずだという、単なる予想にすぎない。）

【結論】
「図形が均一な物質でできている場合の重心」と「図形の中身はスッカラカンで頂点に等しい重りをぶら下げたときの重心」は、一般には一致しない。（三角形の場合はこれがたまたま一致する。）



では、四角形の重心はどのように求めればよいのかと言うと、

四角形をABCDとすると
(1) △ABCの重心G1と、△ACDの重心G2を結ぶ。
次に、
(2) △ABDの重心G3と、△BCDの重心G4を結ぶ。
線分(1)(2)の交点が四角形の重心になる。
なぜならば、図形の重心とは、その図形を１点に凝縮させた点であるので、四角形を三角形２つに分割したわけだから、三角形を凝縮させた点ともう一方の三角形を凝縮させた点の２つを結んだ線上にバランスを取り合ってつりあう点が存在するわけである。
つまり、(1)の上にあり、かつ(2)の上にある点である。（つまり交点）。

また、五角形でも、
四角形と三角形に分割し、重心同士を結び、（四角形の重心の求め方は上と同じ。）
また別のところで四角形と三角形に分割し、重心同士を結び、
その交点です。
（理由は四角形の場合と同じ。）

同様にして、ｎ角形でもこれと同じ方法でできる。

また別の方法もあります。
四角形の場合を例にしますと、三角形二つに分割します。そしてそれぞれの重心を結びます。
面積比について、右の三角形：左の三角形＝m:nでしたら、左からｍ：ｎに内分する点が重心です。
（四角形以外のn角形でも同様。）
（重心さえ求まれば、質量はその一点にすべて集まるのだから、あとは線分の天秤の理論が使える。使えないのは、重心を求めるまでの作業で上記の赤字のようなミスだ。これには気をつける必要がある。）

【３　正四面体と立体図形の重心】
さて、四角形では(a+b+c+d)/4が言えない。
では(a+b+c+d)/4が言えるのはどんな図形なのか？

しつこく次のように考えてみる。
０次元単体(点)の重心は a/1
１次元単体(線分)の重心は (a+b)/2
２次元単体(三角形)の重心は (a+b+c)/3
なのだから、
３次元単体(四面体)の重心は (a+b+c+d)/4
なのではないか？
（さらに、４次元単体（五胞体）の重心は(a+b+c+d+e)/5
ｎ次元単体の重心は(a+b+c+d+e+f+…）/(n+1)）

ということで、まずは最も求めやすい正四面体で、重心を求めてみる。これで重心が(a+b+c+d)/4であることが言えればうれしい。

そこで、まず、考えやすい正四面体で考える。
以下のように合同な４つの立体に分割できるので、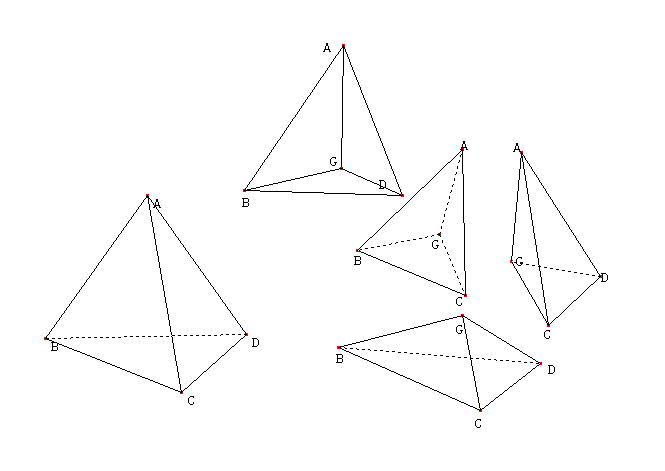
V＝v1+v2+v3+v4
合同に四等分してあるので、元の正四面体の高さをｈとすると、切断された四面体の高さはh/4。
よって、Aから底面BCDに下ろした垂線の足をHとすると、AG：GH＝３：１

また、さらにGを詳しく見てみると、
線分AHを３：１に内分する点Gは
g = (a+3g)/(3+1) = (a+3g)/4 = (1/4)(a+3・(b+c+d)/3)　（小文字は位置ベクトル）
とできることより、(b+c+d)3は底面の重心を表しているので、底面である△BCDの重心と頂点Aを結んだ線分を３：１に内分する点が正四面体の重心であることもわかる。

以上のことより、
正四面体において、
底面の重心と頂点を結んだ線分を１：３に内分する点が重心Gである。
ことが言える。

また、さらに調べると、
g = (a+3g)/(3+1) = (a+3g)/4 = (1/4)(a+3・(b+c+d)/3)　
=(a+b+c+d)/4
以上のことより、
正四面体の重心は (a+b+c+d)/4
であることがわかる。

ここで、カバリエリの原理により、この正四面体をスライドさせてもかまわないので、
正四面体と、それを四つに分割したそれぞれの四面体の体積比も４：１のままである。
また、正四面体のそれぞれの辺がを曲線にならないように、つまり直線であるようにスライドさせるならば、それによって出来上がるものは四面体であり、頂点と底面の重心を結んだ線分も、当然直線であるから、その線分上の重心も、他のスライド面と同じ比率で移動する。
また、切断面の形を変えてもよいわけであるから、以下の２つが言える。

(1) 正四面体と高さと底面積の比が等しい四面体の重心は (a+b+c+d)/4である

(2) 正四面体と高さと底面積の比が等しい錐の重心は、錐と底面の重心を結んだ線分上にあり、１：３に内分する。


さらに、カバリエリの原理は１：１について言及しているが、一般にｍ：ｎでも成り立つことを合わせて考えれば、上記(1)(2)について、「正四面体の高さと底面積の制限」が取れる。
つまり、

(A) 四面体の重心は (a+b+c+d)/4である。

(B) 錐の重心は、錐と底面の重心と頂点を結んだ線分上にあり、高さ1/4のところにある。(１：３に内分する)。

ことが言える。

（※　もう柱の重心は調べるまでもないだろう。）

ところで、上記のように、「カバリエリの定理や積分法」（無限回の操作）なしに、四面体の公式を導くことはできない。
なぜならば、ヒルベルトの２３の問題というものがあり、

このデーンの定理は有限回の操作では、たとえ同じ体積をもっていたとしても分割合同ではない、ということを言っている。
つまり、体積の理論を作るには、無限回の操作（つまり積分法やカバリエリの原理）の助けがどうしても必要となることを意味する。

【パップス・ギュルダンの定理】

半円の重心を初等幾何の範囲で求めることはできないか？
たぶん、できない。


しかし、初等幾何の範囲を超えてもよいのなら、重心の積分の定義を利用して一気に求めればよいわけだが、それ以外の方法として
・パップス・ギュルダンの定理（この証明は高校範囲を超えるが。）　を使う手もある。

(回転体の体積）＝（回転体による図形の重心の軌跡の長さ）×（図形の面積）

さて、これを使いますと、半円を直径を軸に一回転させたものが球ですので、
（球の体積）＝（半円の重心の移動した長さ）×（半円の面積）

で求めることができる。

また、逆に、
（球の体積）＝（半円の重心の移動した長さ）×（半円の面積）
であるから、
（球の体積）と（半円の面積）は既に初等幾何的に、どんな値なのかわかっているので、
このことから（半円の重心の移動距離）を求めることができるので、
（半円の重心）を求めることができる。


また、円弧の重心についても、
パップスギュルダンの定理は、体積だけではなく、表面積や側面積にも使えますので、もし、円弧の重心がわかれば、球の表面積も求めることができるということになります。
（球の表面積）＝（円弧の重心の移動した長さ）×（円弧）

つまり、上と同様にして、パップスギュルダンの定理を使い、円弧の重心も求めることができる。

※　カバリエリの定理は、切断面の面積をスライドさせていくときに、常に切断面が他の切断面に平行に、かつ、切断面の面積が重ならないようにスライドさせたときなら成り立つわけですが、

パップス・ギュルダンの定理は、その切断面のスライドが、他の面と平行でなく、重なっても、それが円運動の場合なら成り立つと言っているわけである。

【三角形の重心が２：１の内分点にあることを漸化式を利用して求める。】

1/2、1/4、3/8、5/16、11/32、…
これは、隣接三項間漸化式
a[n+2]=(1/2)a[n+1]+(1/2)a[n],a[1]=1/2,a[2]=1/4
である。
ここから、一般項a[n]を求めることを考える。

　もとの漸化式を
　　ａ_n+2−αａ_n+1＝β（ａ_n+1−αａ_n）
　の形にすることを考えます。カッコをはずして、
　　ａ_n+2＝（α＋β）ａ_n+1−αβａ_n
　係数を比較して、
　　ｂ＝α＋β、　ｃ＝−αβ
　よって、２次方程式の解と係数の関係より、α、βは２次方程式
　　ｘ²−ｂｘ−ｃ＝０　（特性方程式）
　の解となる。逆に、特性方程式の解をα、βとすると、もとの漸化式は
　　ａ_n+2−αａ_n+1＝β（ａ_n+1−αａ_n）
　　ａ_n+2−βａ_n+1＝α（ａ_n+1−βａ_n）
　と書ける。
　初項、第２項をａ₁、ａ₂ とすると、
　　ａ_n+1−αａ_n＝β^n-1（ａ₂−αａ₁）
　　ａ_n+1−βａ_n＝α^n-1（ａ₂−βａ₁）

　（α≠βのとき）
　両辺の差を取って、
　　（β−α）ａ_n＝β^n-1（ａ₂−αａ₁）−α^n-1（ａ₂−βａ₁）
　より、
　　ａ_n＝｛β^n-1（ａ₂−αａ₁）−α^n-1（ａ₂−βａ₁）｝/（β−α）

ところで、
特性方程式ｘ^2＝ｂｘ＋ｃ の解がα、βであったので、
今、ｂ＝1/2, c=1/2であることを考えると、
x^2=(1/2)x+(1/2)の解がα、βである。
両辺二倍して、整理して、
2x^2-x-1=0
(x-1)(2x+1)=0
これより、
x=1,-1/2
どちらをα、βと置いても一般性を失わないので、
α＝-1/2,β＝１とすると、
a[1]=1/2,a[2]=1/4も考え、★にこれらを代入し、
a[n]={β^(n-1)((1/4)-α(1/2)-α^(n-1)((1/2)-β(1/4)}/(β-α)
={(1/4 + 1/4)+(1/2)^(n-1) (1/2 - 1/4)/(3/2)
=(2/4 + (1/2)^(n-1)・(1/4))/(3/2)
=2(2/4 + (1/2)^(n-1)・(1/4))/3
=(1/2)(2+(1/2)^(n-1))/3
=1/2・2 + (1/2)^n /3
よって、
lim[n→∞]1/2・2 + (1/2)^n /3
=(1+0)/3
=1/3　



五胞体